Сумма внешних углов многоугольника - это важная геометрическая характеристика, которая имеет постоянное значение для любого простого многоугольника (не имеющего самопересечений). Рассмотрим это свойство подробно.
Содержание
Определение внешнего угла
Внешний угол многоугольника - это угол, смежный с внутренним углом многоугольника. Он образуется продолжением одной из сторон и соседней стороной фигуры.
- Каждая вершина многоугольника имеет два возможных внешних угла
- Обычно рассматривают только один внешний угол на вершину
- Внешний угол измеряется между продолжением стороны и соседней стороной
Теорема о сумме внешних углов
| Тип многоугольника | Сумма внешних углов |
| Выпуклый многоугольник | 360° |
| Невыпуклый многоугольник | 360° |
| Многоугольник с самопересечениями | Зависит от конкретной конфигурации |
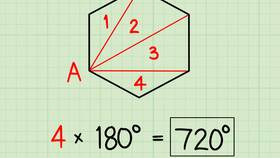
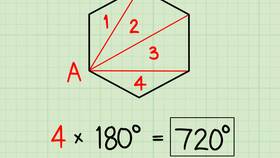
Доказательство теоремы
Рассмотрим доказательство для n-угольника:
- В каждой вершине сумма внутреннего и внешнего углов равна 180°
- Сумма всех таких пар для n вершин: n × 180°
- Сумма внутренних углов: (n - 2) × 180°
- Следовательно, сумма внешних углов: n × 180° - (n - 2) × 180° = 360°
Пример для различных фигур
| Фигура | Количество сторон | Сумма внешних углов |
| Треугольник | 3 | 360° |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 360° |
| Шестиугольник | 6 | 360° |
Особые случаи
- Для правильного n-угольника все внешние углы равны между собой
- Величина каждого внешнего угла правильного многоугольника: 360°/n
- В звездчатых многоугольниках сумма может отличаться от 360°
Практическое значение
Знание суммы внешних углов применяется:
- В архитектуре при проектировании конструкций
- В компьютерной графике при обработке полигонов
- В навигационных расчетах
- При решении геометрических задач
Заключение
Сумма внешних углов любого простого многоугольника всегда равна 360°, независимо от количества его сторон. Это удивительное свойство демонстрирует фундаментальную закономерность в геометрии и находит многочисленные применения в различных областях науки и техники.