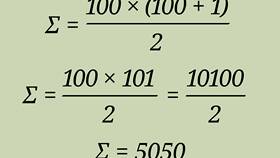Вывод формул для вычисления сумм - важный математический навык, применяемый в алгебре, анализе и дискретной математике. Рассмотрим основные методы вывода формул сумм различных последовательностей.
Содержание
Основные типы сумм
| Тип последовательности | Пример |
| Арифметическая прогрессия | 1 + 2 + 3 + ... + n |
| Геометрическая прогрессия | 1 + 2 + 4 + 8 + ... + 2n |
| Квадраты чисел | 12 + 22 + ... + n2 |
Метод вывода формулы суммы арифметической прогрессии
Алгоритм вывода
- Запишите сумму S = a1 + a2 + ... + an
- Выразите члены через первый член и разность: ak = a1 + (k-1)d
- Запишите сумму в прямом и обратном порядке
- Сложите обе суммы почленно
- Получите 2S = n(a1 + an)
- Выведите окончательную формулу: S = n(a1 + an)/2
Вывод формулы суммы геометрической прогрессии
| Шаг | Действие |
| 1 | Запишите S = a + ar + ar2 + ... + arn |
| 2 | Умножьте обе части на r: rS = ar + ar2 + ... + arn+1 |
| 3 | Вычтите из первого выражения второе |
| 4 | Получите S(1-r) = a(1 - rn+1) |
| 5 | Выразите S: S = a(1 - rn+1)/(1 - r) |
Метод математической индукции
Для доказательства готовых формул сумм:
- Проверьте базу индукции (n=1)
- Предположите верность для n=k
- Докажите для n=k+1
- Сделайте вывод о справедливости для всех n
Суммы специального вида
Сумма квадратов
12 + 22 + ... + n2 = n(n+1)(2n+1)/6
Сумма кубов
13 + 23 + ... + n3 = [n(n+1)/2]2
Телескопические суммы
- Представьте общий член в виде разности
- Запишите развернутую сумму
- Сократите промежуточные члены
- Останется только первый и последний элементы
Применение производящих функций
- Составьте производящую функцию последовательности
- Найдите ее аналитическое выражение
- Преобразуйте для получения суммы
- Выделите нужный коэффициент
Заключение
Вывод формул сумм требует понимания природы последовательности и применения соответствующих математических методов. Освоение этих техник позволяет решать широкий круг задач в математике и ее приложениях, от анализа алгоритмов до финансовых расчетов.